روش دوفازی

فاز1 مسئله را به شکل معادله دربیاورید و متغیر های مصنوعی لازم را به قید ها اضافه کنید (دقیقا مانند روش M) تا راه‌حل پایه را برای شروع تضمین کند. در مرحله‌ی بعد، یک راه‌جل پایه از معادلات بدست آمده بیابید تا همیشه مجموع متغیرهای مصنوعی را به حداقل برساند. صرف نظر از اینکه LP در بیشینه یا کمینه باشد. اگر میزان حداقل مجموع مثبت بود، مسئله LP جواب عملی ندارد، در غیر اینصورت به فاز دو مراجعه کنید.

فاز2 از راه‌حل امکان‌پذیر فاز 1 به عنوان راه‌حل پایه اولیه برای مسئله‌ی عملی استفاده کنید.

ملاحظات حذف متغیرهای مصنوعی و ستون‌های آنها در پایان فاز 2 تنها زمانی می‌تواند انجام شود که همه‌ی آن متغیرهای مصنوعی غیرپایه‌ای باشند. اگر در انتها فاز 2 یک یا بیشتر متغیر مصنوعی در پایه وجود داشته باشد، (در سطح صفر) حذف آنها به مراحل اضافی زیر نیاز دارد:

گام1 یک متغیر مصنوعی صفر برای خروج از راه‌جل پایه انتخاب کنید و سطر آن را به عنوان سطر لولا تعیین کنید. متغیر ورودی می‌تواند هر متغیر پایه‌ای غیرمصنوعی و با ضریب غیرصفر (مثبت یا منفی) در سطر لولا باشد. تکرار سیمپلکس مربوطه را انجام دهید.

گام2 ستون متغیر مصنوعی (فقط خروج) را از تابلو حذف کنید. اگر تمام متغیرهای مصنوعی صفر حذف شده‌اند، با فاز دوم بروید و در غیر این صورت به گام 1 برگردید.

مشکل روش M یزرگ این است که انتخاب M کاملا قضاوتی است و از لحاظ کامپیوتری و سیستمی مشکل دارد و ماشین کامپیوتری قادر به تشخیص مقدار M نخواهد بود.

مثال21

Minimize \(z=4*x_1+x_2\)

\(x_1+2*x_2 \leq 4\)

\(3*x_1+x_2 = 3\)

\(4*x_1+3*x_2 \geq 6\)

جواب21

فرم جبری

Minimize \(z-4*x_1-x_2=0\)
\(x_1+2*x_2+s_1=4\)
\(x_1+x_2+R_1=3\)
\(4*x_1+3*x_2-s_2+R_2=6\)

فاز 1

تابع هدف در فاز1

min \(z=R_1+R_2\)
فرم جبری \(z-R_1-R_2=0\)
جدول را بر این اساس تشکیل می‌دهیم.

جدول فاز اول

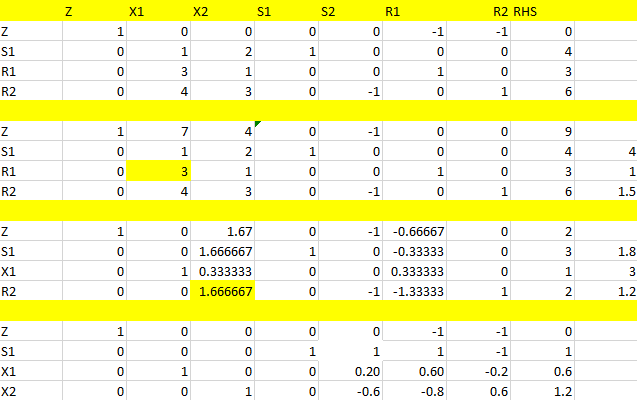
فاز 2

ردیف Z جدول آخر فاز 1 که به جواب رسیدیم را پاک کرده و Z اصلی‌مان را جایگذاری می‌کنیم.

مثال22

Minimize \(z=6*x_1+3*x_2\)

\(x_1+x_2 \geq 1\)

\(2*x_1-x_2 \geq 1\)

\(3*x_2 \leq 2\)

جواب22

فرم جبری

Minimize \(z-6*x_1-3*x_2=0\)
\(x_1+x_2-s_1+R_1=1\)
\(2*x_1-x_2-s_2+R_2=1\)
\(3*x_2+s_3=2\)

فاز 1

تابع هدف در فاز1

min \(z=R_1+R_2\)
فرم جبری \(z-R_1-R_2=0\)
جدول را بر این اساس تشکیل می‌دهیم.

فاز 2

ردیف Z جدول آخر فاز 1 که به جواب رسیدیم را پاک کرده و Z اصلی‌مان را جایگذاری می‌کنیم.

مثال23

Minimize \(z=-3*x_1+x_2-2*x_3\)

\(x_1+3*x_2+x_3 \leq 5\)

\(2*x_1-x_2+x_3 \geq 2\)

\(4*x_1+3*x_2-2*x_3 = 5\)

جواب21

فرم جبری

Minimize \(z+3*x_1-x_2+2*x_3-M*R_1-M*R_2=0\)
\(x_1+3*x_2+x_3+s_1=5\)
\(2*x_1-x_2+x_3-s_2+R_1=2\)
\(4*x_1+3*x_2-2*x_3+R_2=5\)

فاز 1

تابع هدف در فاز1

min \(z=R_1+R_2\)
فرم جبری \(z-R_1-R_2=0\)
جدول را بر این اساس تشکیل می‌دهیم.

فاز 2

ردیف Z جدول آخر فاز 1 که به جواب رسیدیم را پاک کرده و Z اصلی‌مان را جایگذاری می‌کنیم.