روش M بزرگ

روش M با LP به شکل معادله شروع می‌شود. اگر معادله i یک متغیر کمکی نداشته باشد (یا متغیری که نقش کمکی را بازی کند.)، یک متغیر مصنوعی \(R_i\) اضافه می‌شود تا یک راه‌حل شروعی شبیه به راه‌حل همه کمکی (all-slack) پدید آید. به هر حال، به خاطر اینکه متغیرهای مصنوعی جزئی از مسئله اصلی نیستند؛ به یک ترفند مدلسازی نیاز است تا آن ها را در زمان رسیدن به تکرار بهینه به صفر برساند. (با فرض اینکه برای مشکل یک راه‌حل عملی وجود داشته باشد) هدف موردنظر با تخصیص جریمه تعریف شده به این صورت جاصل می‌شود:
-ضریب تابع هدف متغیر مصنوعی
- در مسائل بیشینه‌سازی \(-M\)
- در مسائل کمینه سازی M
- M یک مقدار مثبت و بزرگ است (از لحاظ ریاضی به سمت مثبت بی‌نهایت سوق میکند.)
0

مثال17

Minimize \(z=4*x_1+x_2\)

\(x_1+2*x_2 \leq 4\)

\(3*x_1+x_2 = 3\)

\(4*x_1+3*x_2 \geq 6\)

جواب17

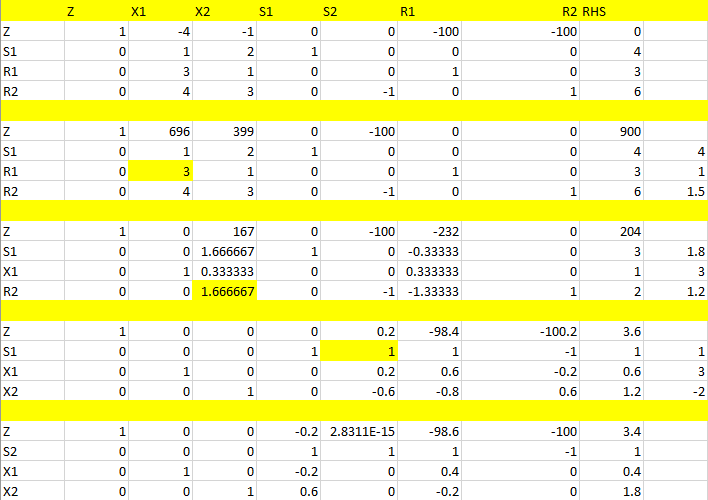
فرم جبری

Minimize \(z-4*x_1-x_2-M*R_1-M*R_2=0\)
\(x_1-2*x_2+s_1=4\)
\(3*x_1+x_2+R_1=3\)
\(4*x_1+3*x_2-s_2+R_2=6\)

جداول

مثال18

Minimize \(z=6*x_1+3*x_2\)

\(x_1+x_2 \geq 1\)

\(2*x_1-x_2 \geq 1\)

\(3*x_2 \leq 2\)

جواب18

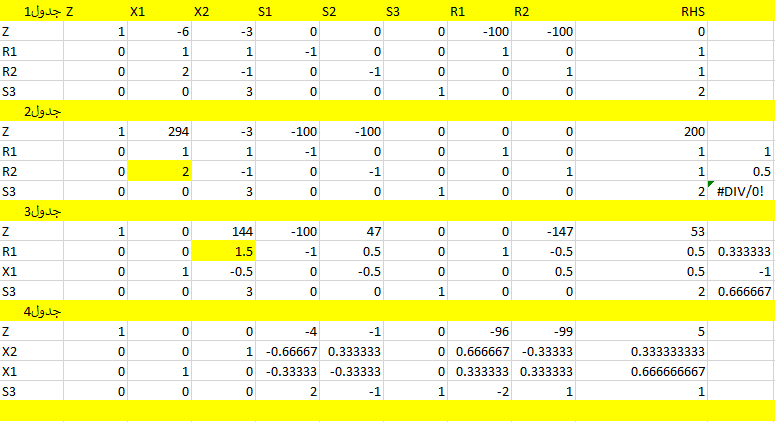
فرم جبری

Minimize \(z-6*x_1-3*x_2-M*R_1-M*R_2=0\)
\(x_1+x_2-s_1+R_1=1\)
\(2*x_1-x_2-s_2+R_2=1\)
\(3*x_2+s_3=2\)

جداول

مثال19

Minimize \(z=-3*x_1+x_2-2*x_3\)

\(x_1+3*x_2+x_3 \leq 5\)

\(2*x_1-x_2+x_3 \geq 2\)

\(4*x_1+3*x_2-2*x_3 = 5\)

جواب19

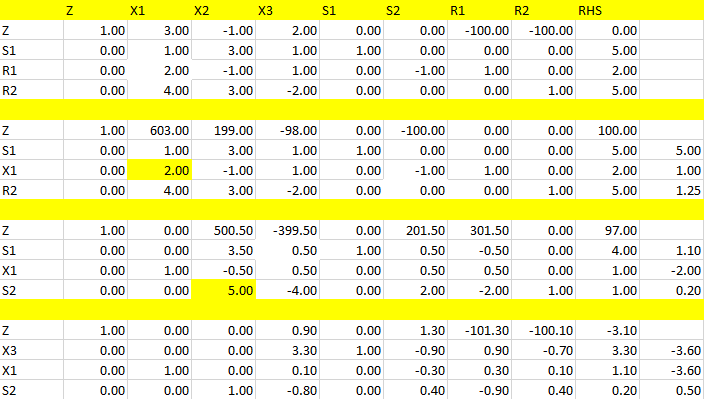
فرم جبری

Minimize \(z+3*x_1-x_2+2*x_3-M*R_1-M*R_2=0\)
\(x_1+3*x_2+x_3+s_1=5\)
\(2*x_1-x_2+x_3-s_2+R_1=2\)
\(4*x_1+3*x_2-2*x_3+R_2=5\)

جداول

مثال20

Minimize \(z=0.3*x_1+0.9*x_2\)

\(x_1+x_2 \geq 800\)

\(0.21*x_1-0.3*x_2 \leq 0\)

\(0.03*x_1-0.01*x_2 \geq 0\)

جواب20

فرم جبری

Minimize \(z-0.3*x_1-0.9*x_2-M*R_1=0\)
\(x_1+x_2-s_1+R_1=800\)
\(0.21*x_1-0.3*x_2+s_2=0\)
\(0.03*x_1-0.01*x_2+s_3=0\)