الگوریتم سیمپلکس

شرایط بهینه متغیر ورودی در مسئله‌ی بیشینه‌سازی (یا کمینه‌سازی) متغیر غیرپایه‌ای است که بیشترین ضریب منفی (یا مثبت) در سطر z دارد. مساوی ها به صورت خودکار از بین می‌روند. بهینه‌سازی در تکرار بدست می‌آید که در آن همه‌ی ضرایب سطر z غیرمنفی (یا غیرمثبت) هستند.

شرط امکان‌سنجی برای هر 2 مسئله‌ی بهینه‌سازی متغیر خروجی همان متغیر پایه است که با کوچکترین نسبت غیرمنفی با مخرج کاملا مثبت همراه است. مساوی ها به صورت خودکار از بین می‌روند.

عملیات سطر گاوس-جردن

-سطر لولا
-متغیر خروجی در ستون Basic را با متغیر ورودی جابهجا کنید.
-سطر لولای جدید= سطر لولای حاضر / عنصر لولا
-تمامی سطرهای دیگر، از جمله z
-سطر جدید = سطر حاضر - ضریب ستون لولای آن * سطر لولای جدید

الگوریتم
گام 1- نوشتن ضابطه ها به فرم جبری
گام 2- تشکیل جدول سیمپلکس
گام 3- انتخاب متغیر های نماینده
گام 4- ستون لولا را مشخص می‌کنیم - در ماکزیمم‌سازی عبارت است از ستونی با منفی ترین عدد ردیف z
- در مینیمم‌سازی عبارت است از ستونی با مثبت ترین عدد ردیف z
گام 5- انتخاب ردیف لولا (کوچکترین عدد نامنفی بین اعداد سمت راست تقسیم بر اعداد ستون لولا)
گام 6- عدد لولا برابر با عدد تلاقی ستون لولا و ردیف لولاست
گام 7- در جدول جدید عدد لولا را برابر 1 می‌کنیم (با تقسیم بر خودش) و در نتیجه ردیف لولا نیز بر عدد لولا تقسیم می‌شود.
گام 8- سایر ضرایب ستون لولا برابر با صفر شوند. (پیدا کردن ضریبی که در عدد لولا جدید (یعنی 1) ضرب شده و با ردیف مورد نظر جمع شود تا عدد ستون لولای جدول جدید صفر باشد)
گام 9- جاگزینی متغیر ستون لولا به جای متغیر نماینده ردیف لولا
گام 10- شرط خاتمه - اگر در ماکزیمم‌سازی ردیف z مثبت شدند الگوریتم خاتمه پیدا می‌کند اما اگر چنین نشد عدد لولا جدیدی پیدا می‌کنیم و جدول جدیدی تولید می‌کنیم.
- اگز در مینیمم‌سازی ردیف z همگی منفی شدند، الگوریتم خاتمه پیدا می‌کند وگرنه با پیدا کردن عذذ لولا جدید و تشکیل جدول دیگری الگوریتم را تکرار می‌کنیم.

مثال13

به روش سیمپلکس مثال12 را حل کنید.

Maximize \(z=2*x_1+3*x_2\)

\(2*x_1+x_2 \leq 4\)

\(x_1+2*x_2 \leq 5\)

\(x_1,x_2 \geq 0\)

جواب13

فرم جبری

Maximize \(z-2*x_1-3*x_2=0\)
\(2*x_1+x_2+s_1=4\)
\(x_1+2*x_2+s_2=5\)

مثال14

مسئله‌ی بهرنگ را به روش سیمپلکس حل کنید.

Maximize \(z=5*x_1+4*x_2\)

\(6*x_1+4*x_2 \leq 24\)

\(x_1+2*x_2 \leq 6\)

\(-x_1+x_2 \leq 1\)

\(x_2 \leq 2\)

\(x_1,x_2 \leq 0\)

جواب14

فرم جبری

Maximize \(z-5*x_1-4*x_2=0\)
\(6*x_1+4*x_2+s_1=24\)
\(x_1+2*x_2+s_2=6\)
\(-x_1+x_2+s_3=1\)
\(x_2+s_4=2\)

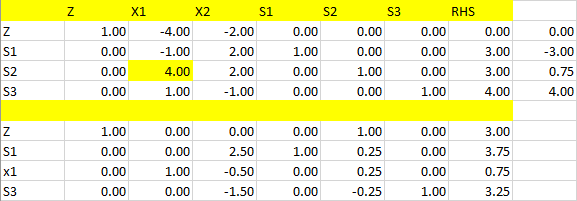
جداول

مثال15

Maximize \(z=3*x_1+2*x_2\)

\(-x_1+2*x_2 \leq 4\)

\(3*x_1+2*x_2 \leq 4\)

\(x_1-x_2 \leq 3\)

جواب15

فرم جبری

Maximize \(z-3*x_1-2*x_2=0\)
\(-x_1+2*x_2+s_1=4\)
\(3*x_1+2*x_2+s_2=4\)
\(x_1-x_2+s_3=3\)

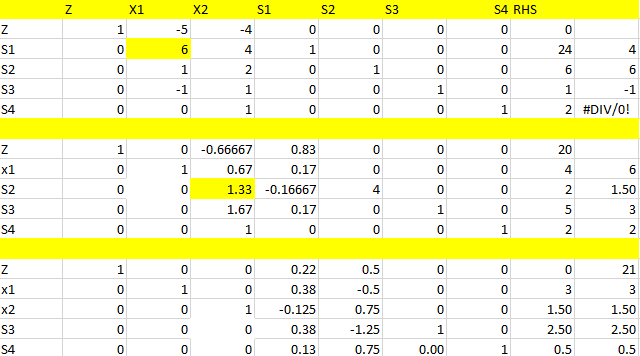
جداول

مثال16

Maximize \(z=3*x_1+2*x_2+5*x_3\)

\(3*x_1+2*x_3 \leq 460\)

\(x_1+2*x_2+x_3 \leq 430\)

\(x_1+4*x_2 \leq 420\)

جواب16

فرم جبری

Maximize \(z-3*x_1-2*x_2-5*x_3=0\)
\(3*x_1+2*x_3+s_1=460\)
\(x_1+2*x_2+x_3+s_2=430\)
\(x_1+4*x_2+s_3=420\)

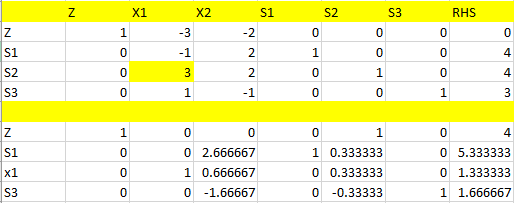
جداول

مثال

Maximize \(z=4*x_1+2*x_2\)

\(-x_1+2*x_2 \leq 3\)

\(4*x_1+2*x_2 \leq 3\)

\(x_1-x_2 \leq 4\)

جواب

فرم جبری

Maximize \(z-4*x_1-2*x_2=0\)
\(-x_1+2*x_2+s_1=6\)
\(4*x_1+2*x_2+s_2=6\)
\(x_1-x_2+s_3=4\)

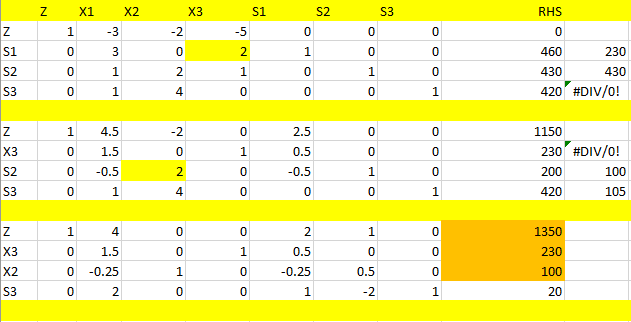
جداول