مثال‌های کاربردی (ادامه)

مثال8(برنامه‌ریزی شهری)

شورای شهر سمنان با کسری بودجه به عنوان یک راهکار بلندمدت پیشنهادی مبنی بر توسعه‌ی فضای مسکونی و نوسازی آن ، اخذ مالیات از ساکنین بیان کرده است. این پیشنهاد شامل دو فاز است؛ فاز اول تخریب منازل غیراستاندارد برای تامین زمین موردنیاز و فاز دوم ساخت و ساز در فضای تامین شده است. خلاصه‌ی شرایط به صورت زیر:
اگر 300 ساختمان تخریب شود و به ازای هر ساختمان غیراستاندارد 0.25 جریب فضا آزاد می‌شود. هزینه تخریب هر خانه 2000 دلار است.
فضای مورد نیاز برای خانه‌های تک، دو، سه و چهار نفره به ترتیب برابر 0.18، 0.28، 0.4 و 0.5 جریب می‌باشد. فضای باز برای امکانات رفاهی 15 درصد در نظر گرفته شده است. هر جریب حدود 4000 \(m^2\) است.
در این طرح خانه های سه و چهار نفره حداقل 25 درصد کل خانه ها را شامل می‌‍شود. واحد های تک نفره حداقل 20 درصد و دو نفره هم 10 درصد.
مالیات خانه های تک، دو، سه و چهار نفره به ترتیب 50، 70، 130 و 160 هزار دلار است.
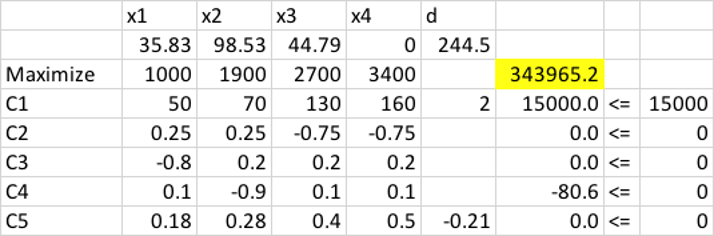
اگر حداکثر وام قابل دریافت از بانک 15 میلیون دلار باشد؛ تعداد خانه‌های تک، دو، سه و چهار نفره را طوری بیابید که حداکثر مالیات حاصل شود.

جواب 8

متغیرهای مستقل

متغیر	شرح
\(x_1\)	تعداد خانه های یک نفره
\(x_2\)	تعداد خانه های دو نفره
\(x_3\)	تعداد خانه های سه نفره
\(x_4\)	تعداد خانه های چهار نفره

متغیر وابسته (حداکثر مالیات)

\(z=1000*x_1+1900*x_2+2700*x_3+3400*x_4\)

قیود

قید	رابطه
\(C_1\)	\(0.28*x_2 \geq 0.1*(0.18*x_1+0.28*x_2+0.4*x_3+0.5*x_4)\)
\(C_2\)	\(0.18*x_1 \geq 0.2*(0.18*x_1+0.28*x_2+0.4*x_3+0.5*x_4)\)
\(C_3\)	\(0.4*x_3+0.5*x_4 \geq 0.25*(0.18*x_1+0.28*x_2+0.4*x_3+0.5*x_4)\)
\(C_4\)	\(50*x_1+70*x_2+130*x_3+160*x_4+300*x_2 \l 15000000\)
\(C_5\)	\(0.18*x_1+0.28*x_2+0.4*x_3+0.5*x_4 \leq 300*0.25*(1*0.15)\)

مثال9(پالایشگاه)

پالایشگاه نقت شیل واقع در جزیره آروبا، ظرفیت تولید 1500000 بشکه نفت خام در روز را دارد. محصولات شیمیایی پالایشگاه شامل 3 نوع بنزین بدون سرب با اعداد اکتان مختلف است؛ بنزین اکتان 87 معمولی، بنزین اکتان 89 پرمیوم، بنزین اکتان 92 سوپر.
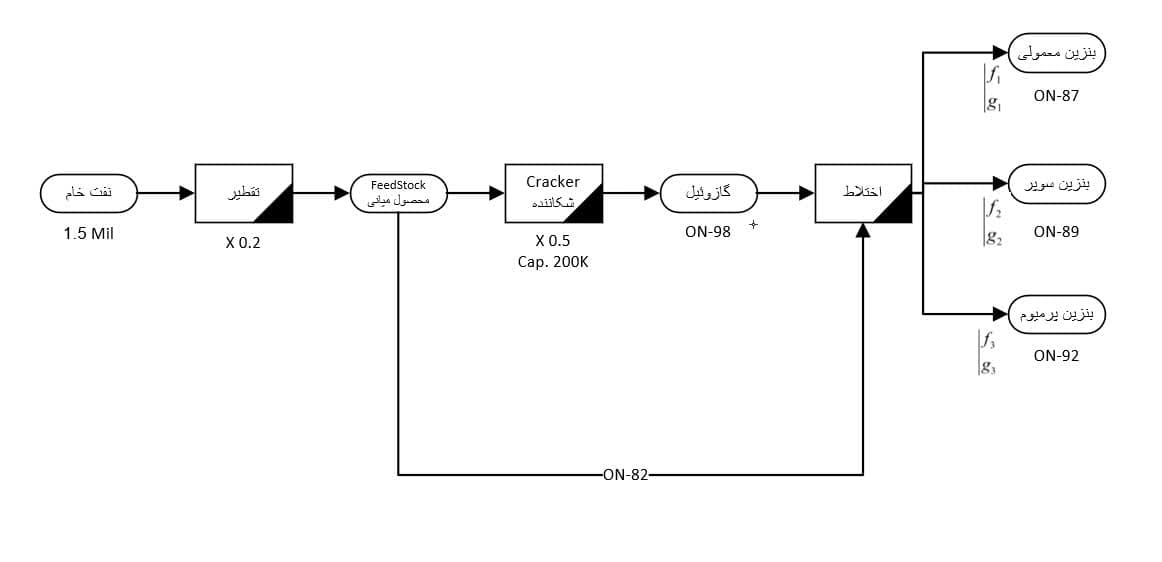
فرآیند پالایش شامل 3 مرحله است؛ مرحله اول برج تقطیر که از هر بشکه نفت خام، 0.2 بشکه مواد میانی با اکتان 82 تولید می‌کند. مرحله دوم واحد کرکر با نسبتی از مواد میانی تولید شده در برج تقطیر با نرخ 0.5 بشکه به ازای هر بشکه مواد میانی، گازوئیل با اکتان 98 تولید می‌کند. مرحله سوم واحد مخلوط کردن که گازوئیل بدست‌آمده از واحد کرکر را با مواد میانی برج تقطیر مخلوط می‌کنند. شرکت تخمین می‌زند که سود خالص به ازای هر بشکه از 3 نوع بنزین را 6.70، 7.20 و 8.10 دلار باشد. ظرفیت ورودی واحد کراکر 200000 بشکه مواد میانی در روز است. تقاضا برای بنزین معمولی، پرمیوم و سوپر به ترتیب 50000، 30000 و 40000 بشکه در روز است. یک مدل بهینه برای بیشترین مقدار تولید ممکن پالایشگاه بنویسید.

جواب 9

دیاگرام تولید به شرح زیر است:

متغیرهای مستقل

متغیر	شرح
\(f_1\)	نسبت مورد نیاز محصول میانی برای بنزین معمولی
\(f_2\)	نسبت مورد نیاز محصول میانی برای بنزین سوپر
\(f_3\)	نسبت مورد نیاز محصول میانی برای بنزین پرمیوم
\(g_1\)	نسبت مورد نیاز گازوئیل برای بنزین معمولی
\(g_2\)	نسبت مورد نیاز گازوئیل برای بنزین سوپر
\(g_3\)	نسبت مورد نیاز گازوئیل برای بنزین پرمیوم

متغیر وابسته

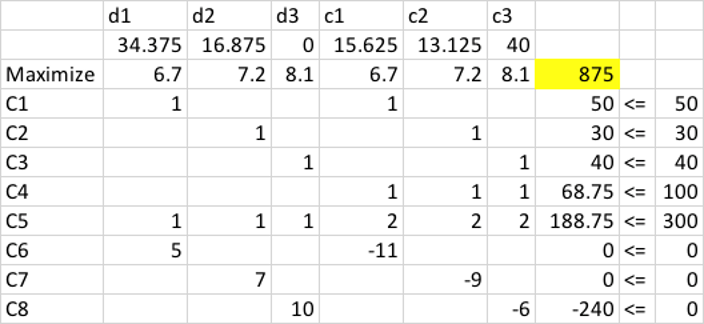
\(z=6.7*(f_1+g_1)+7.2*(f_2+g_2)+8.1*(f_3+g_3)\)

قیود

قید	رابطه
\(C_1\)	\(g_1+g_2+g_3 \leq 200000*0.5\)
\(C_2\)	\(f_1+f_2+f_3+g_1+g_2+g_3 \leq 1500000*0.2\)
\(C_3\)	\(82*f_1+98*g_1 = 87*(f_1+g_1)\)
\(C_4\)	\(82*f_2+98*g_2 = 89*(f_2+g_2)\)
\(C_5\)	\(82*f_3+98*g_3 = 92*(f_3+g_3)\)

مثال10

یک کارخانه با استفاده از 2 ماشین دو محصول تولید می‌کند. هر محصول یک، نیاز به 50 دقیقه در ماشین اول و 30 دقیقه پردازش در ماشین دوم دارد. هر محصول دو، باید 30 دقیقه در ماشین اول و35 دقیقه در ماشین دوم پردازش شوند.
در شروع هفته جاری 60 محصول نوع یک و 85 محصول نوع دو در انبار وجود دارد. زمان آزاد ماشین اول 40 ساعت پیش‌بینی شده و تایم آزاد ماشین دوم 35 ساعت پیش‌بینی شده است. تقاضای محصول نوع یک در هفته جاری 75 واحد و محصول نوع دو 95 واحد بیان شده. سیاست کارخانه این است که مجموع محصولات نوع یک و دو تا آخر این هفته در انبار به حداکثر برساند.

	ماشین 1	ماشین2	موجودی	تقاضا
\(p_1\)	50 min	30 min	60	75
\(p_2\)	30 min	35 min	85	95
دسترسی	40 hr	35 hr

جواب 10

متغیرهای مستقل

متغیر	شرح
\(p_1\)	تعداد تولیدی محصول یک
\(p_2\)	تعداد تولیدی محصول دو

متغیر وابسته
ماکزیمم‌سازی

\(z=p_1+p_2+60+85\)

قیود

قید	رابطه
\(C_1\)	\(p_1 \geq 15\)
\(C_2\)	\(p_2 \geq 10\)
\(C_3\)	\(5*p_1+3*p_2 \leq 240\)
\(C_4\)	\(6*p_1+7*p_2 \leq 420\)

مثال11

یک کمپانی دو محصول A و B را می‌سازد. سود هر محصول نیز به ترتیب 3 یورو و 5 یورو می‌باشد. هر محصول باید در یک ماشین خاص مونتاژ شود. هر دانه محصول A برای سر هم‌شدن 12 دقیقه طول می‌کشد و برای محصول B هم 25 دقیقه. ساعت کاری موثر این ماشین برای جلوگیری از خرابی دستگاه 30 ساعت در هفته تخمین زده شده است. همچنین محدودیت تکنولوژی بنا می‌دارد که به ازای هر 5 محصول A که مونتاژ می‌شود حداقل 2 محصول B باید تولید شود. توسط برنامه ی خطی تعداد تولید هر محصول را بهینه کنید.

جواب 11

متغیرهای مستقل

متغیر	شرح
A	تعداد محصول تولیدی
B	تعداد محصول تولیدی

متغیر وابسته
ماکزیمم‌سازی

\(z=3*A+5*B\)

قیود

قید	رابطه
\(C_1\)	\(12*A+25*B \leq 30*60\)
\(C_2\)	\(2*A \leq 5*B\)