مثال‌های کاربردی

• سرمایه‌گذاری
• برنامه‌ریزی تولید و انبار
• برنامه‌ریزی منابع اصلی
• برنامه‌ریزی توسعه شهری
• فرآورده‌های نفتی و پالایشگاهی

مثال3 (سرمایه‌گذاری)

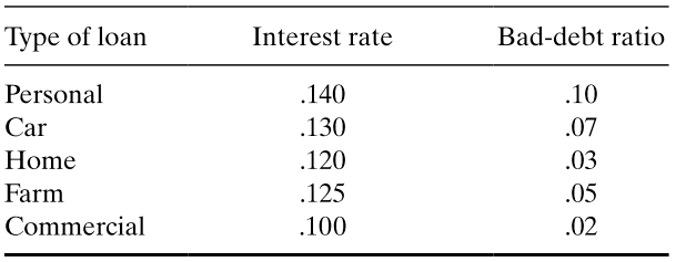
بانک ملی قصد داردطرح وامی را با سرمایه 12 میلیون دلار تدوین کند.در این طرح به شرح زیر به حوزه های مختلف وام داده می‌شود.(اشخاص، خودرو، مسکن، کشاورزی، تجاری) رقابت با سایر موسسات مالی الزام می‌کند که حداقل 40 درصد وام به بخش‌های کشاورزی و تجاری تخصیص داده شود. برای کمک به مسکن نیز وام منزل باید حداقل نصف وام‌های شخصی، خودرو و منزل را شامل شود. اگر بد حسابی غیرقابل بازگشت بوده و سهم آن حداقل 4 درصد وام باشد، سیاست وام دهی را برای این بانک به صورت بهینه تعیین کنید.

نوع وام	بهره	بدحسابی
شخصی	0.140	0.10
خودرو	0.130	0.07
منزل	0.120	0.03
کشاورزی	0.125	0.05
تجاری	0.100	0.02

جواب

متغیرهای مستقل

شخصی	خودرو	منزل	کشاورزی	تجاری
\(x_1\)	\(x_2\)	\(x_3\)	\(x_4\)	\(x_5\)

متغیر وابسته (سود)

\(Z=0.14*(1-0.1)*x_1\)

\(+0.13*(1-0.07)*x_2\)

\(+0.12*(1-0.03)*x_3\)

\(+0.125*(1-0.05)*x_4\)

\(+0.1*(1-0.02)*x_5\)

قیود

قید	رابطه
\(C_1\)	\(x_4+x_5 \geq 0.4*(x_1+x_2+x_3+x_4+x_5)\)
\(C_2\)	\(x_3 \geq 0.5*(x_1+x_2+x_3)\)
\(C_3\)	\(0.1*x_1+0.07*x_2+0.03*x_3+0.05*x_4+0.02*x_5 \leq 0.04*(x_1+x_2+x_3+x_4+x_5)\)
\(C_4\)	\((x_1+x_2+x_3+x_4+x_5) \leq 12000000\)

جواب نهایی (توسط اکسل)

مثال4 (تولید تک‌دوره‌ای)

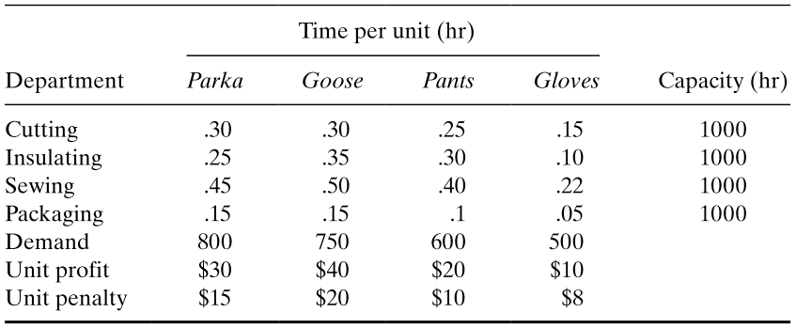
یک شرکت تولیدی لباس برای شروع فصل زمستان قصد تولید اورکت پوست و پر ، شلوار گرم و دستکش دارد. تمامی محصولات نیاز به چهار قسمت برش، لایه‌‌کذاری، دوخت و بسته‌بندی دارد. این شرکت سفارشی دریافت کرده که اگر مقدار مشخص را تحویل ندهد جریمه خواهد شد. طبق جدول زیر تولید این شرکت را بهینه کنید.

فعالیت	پوست	پر	شلوار	دستکش	ظرفیت تولید
برش	0.30	0.30	0.25	0.15	1000
آستر	0.25	0.35	0.30	0.10	1000
دوخت	0.45	0.50	0.40	0.22	1000
بسته‌بندی	0.15	0.15	0.10	0.05	1000
نیاز	800	750	600	500
سود هر فروش	30	40	20	10
جریمه	15	20	10	8

جواب ۴

متغیرهای مستقل

\(x_1\)	\(x_2\)	\(x_3\)	\(x_4\)
پوست	پر	شلوار	دستکش

متغیر وابسته (سود)

\(Z=30*x_1+40*x_2+20*x_3+10*x_4\)

\(-{15*(800-x_1)+20*(750-x_2)+10*(600-x_3)+8*(500-x_4)}\)

قیود

قید	رابطه
\(C_1\)	\(0.3*x_1+0.3*x_2+0.25*x_3+0.15*x_4 \leq 1000\)
\(C_2\)	\(0.25*x_1+0.35*x_2+0.3*x_3+0.1*x_4 \leq 1000\)
\(C_3\)	\(0.45*x_1+0.5*x_2+0.4*x_3+0.22*x_4 \leq 1000\)
\(C_4\)	\(0.15*x_1+0.15*x_2+0.10*x_3+0.05*x_4 \leq 1000\)
\(C_5\)	\(x_1 \leq 800\)
\(C_6\)	\(x_2 \leq 750\)
\(C_7\)	\(x_3 \leq 600\)
\(C_8\)	\(x_4 \leq 500\)

پاسخ کتاب

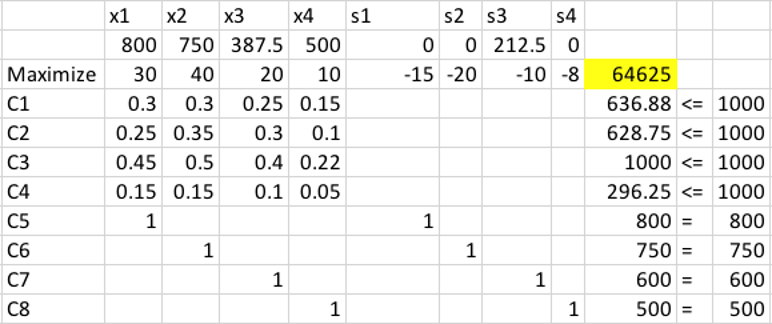
پاسخ دیگر

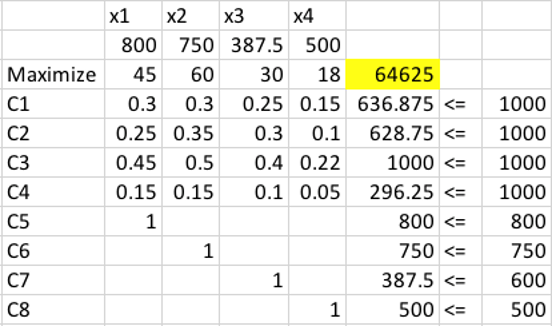
مثال5(تولید چنددوره‌ای)

شرکت تولیدی اکمه قراردادی 6 ماهه مبنی بر تولید 100، 250، 190، 140، 220 و 110 پنجره ی خانگی دارد. هزینه‌ی تولید در این شش ماه عبارت است از 50، 45، 55، 48، 52 و 50 دلار است. این شرکت می‌تواند به منظور استفاده از نوسان قیمت ساخت، تولید ماهانه خود را بیشتراز نیاز ماهانه کند. البته هزینه انبار کردن هر پنجره‌ی اصافی 8 دلار در ماه است. برنامه‌ی تولیدی این کارخانه در مدت شش ماه را بهینه کنید.

جواب ۵

ماه	1	2	3	4	5	6
تقاضا	100	250	190	140	220	110
هزینه	50	45	55	48	52	50
انبار	8	8	8	8	8	8

متغیرهای مستقل

متغیر	شرح
\(x_1\)	تولید ماه اول
\(x_2\)	تولید ماه دوم
\(x_3\)	تولید ماه سوم
\(x_4\)	تولید ماه چهارم
\(x_5\)	تولید ماه پنجم
\(x_6\)	تولید ماه ششم

متغیر وابسته (هزینه)

\(Z = 50 * x_1 + 45 * x_2 + 55 * x_3 + 48 * x_4 + 52 * x_5 + 50 * x_6\)

\(+ 8 * (x_1 - 100)\)

\(+ 8 * (x_1 + x_2 - 100 - 250)\)

\(+ 8 * (x_1 + x_2 + x_3 - 100 - 250 - 190)\)

\(+ 8 * (x_1 + x_2 + x_3 + x_4 - 100 - 250 - 190 - 140)\)

\(+ 8 * (x_1 + x_2 + x_3 + x_4 x_5 - 100 - 250 - 190 - 140 - 220)\)

\(+ 8 * (x_1 + x_2 + x_3 + x_4 + x_5+ x_6 - 100 - 250 - 190 - 140 - 220 - 110)\)

قیود

قید	رابطه
\(C_1\)	\(x_1 \geq 100\)
\(C_2\)	\(x_1+x_2 \geq 100+250\)
\(C_3\)	\(x_1+x_2+x_3 \geq 100+250+190\)
\(C_4\)	\(x_1+x_2+x_3+x_4 \geq 100+250+190+140\)
\(C_5\)	\(x_1+x_2+x_3+x_4+x_5 \geq 100+250+190+140+220\)
\(C_6\)	\(x_1+x_2+x_3+x_4+x_5+x_6 \geq 100+250+190+140+220+110\)

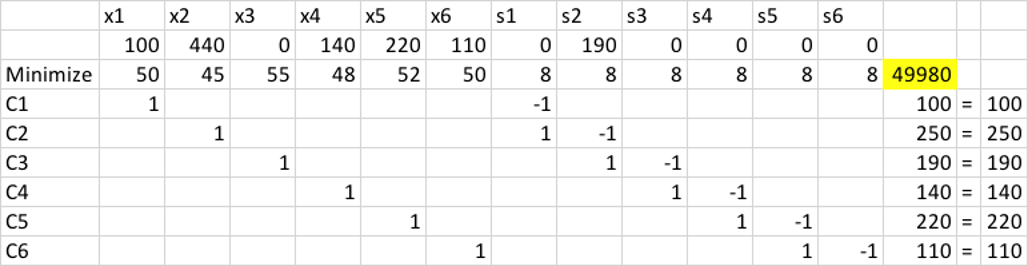
مثال6 (تسطیح منابع)

محصولی را در ماه های فروردین، اردیبهشت، خرداد و تیر تولید می‌کنیم. میزان تقاضا در هر یک از ماه‌ها به ترتیب 520،720،520،620 واحد می‌باشد. این شرکت 10 پرسنل ثابت دارد و می‌تواند پرسنل موقت استخدام نماید. هزینه استخدام و تعدیل به ترتیب 200 و 400 دلار است. هر پرسنل ثابت در ماه 12 محصول تولید می‌کند درحالیکه پرسنل موقت در همان مدت 10 محصول تولید می‌کند. این شرکت می‌تواند بیش از حد تقاضا تولید کرده و انبار نماید. هزینه انبار 50 دلار در ماه است. سیستم استخدام و تعدیل بهینه برای این شرکت تعیین کنید.

جواب6

چون تولید پرسنل ثابت در هزینه تاثیری ندارد پس تولید آنها را از تقاضا کم می‌کنیم

متغیرهای مستقل

	فروردین	اردیبهشت	خرداد	تیر
استخدام	\(h_1\)	\(h_2\)	\(h_3\)	\(h_4\)
تعدیل	\(f_1\)	\(f_2\)	\(f_3\)	\(f_4\)
انبار	\(s_1\)	\(s_2\)	\(s_3\)	\(s_4\)
تقاضا	400	600	400	500

متغیرهای وابسته (هزینه)

\(z=200*(h_1+h_2+h_3+h_4)\)

\(+400*(f_1+f_2+f_3+f_4)\)

\(+50*(s_1+s_2+s_3+s_4)\)

قیود

قید	رابطه
\(C_1\)	\(10*(h_1-f_1)-400=s_1\)
\(C_2\)	\(10*(h_1+h_2-f_1-f_2)-600+s_1=s_2\)
\(C_3\)	\(10*(h_1+h_2+h_3-f_1-f_2-f_3)-400+s_1+s_2=s_3\)
\(C_4\)	\(10*(h_1+h_2+h_3+h_4-f_1-f_2-f_3-f_4)-500+s_1+s_2+s_3=s_4\)

جواب نهایی(توسط اکسل)

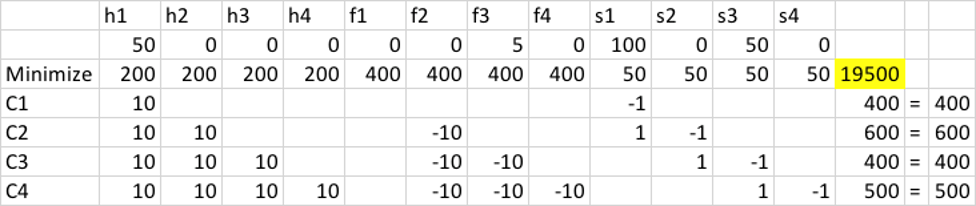
مثال7 (برنامه حمل و نقل)

شهرداری سمنان درحال امکان‌سنجی ارتقای سیستم حمل و نقل عمومی می‌باشد. هدف این امکان‌سنجی پیداکردن تعداد حداقل اتوبوس های موردنیاز برای پاسخگویی به نیاز های حمل و نقل است. آمار گرفته شده نشان می‌دهد که تعداد اتوبوس مورد نیاز در روز نوسان دارد. بر اساس این داده ها تقاضای اتوبوس در بازه ی 4 ساعته به صورت شکل زیر داده شده است. با فرض اینکه هر اتوبوس بعد از 8 ساعت نیاز به استراحت دارد، برنامه‌ی بهینه اتوبوس ها را مشخص کنید.

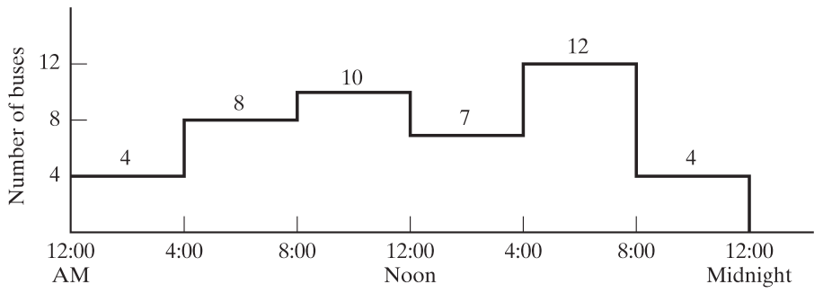
جواب7

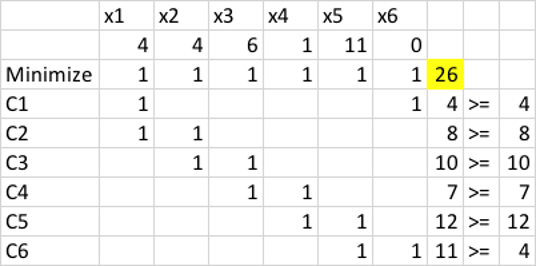
متغیر های مستقل

متغیر	شرح
\(x_1\)	اتوبوس وارد مدار شده ساعت 12 شب
\(x_2\)	اتوبوس وارد مدار شده ساعت 4 صبح
\(x_3\)	اتوبوس وارد مدار شده ساعت 8 صبح
\(x_4\)	اتوبوس وارد مدار شده ساعت 12 ظهر
\(x_5\)	اتوبوس وارد مدار شده ساعت 4 بعدازظهر
\(x_6\)	اتوبوس وارد مدار شده ساعت 8 شب

متغیرهای وابسته

\(z=x_1+x_2+x_3+x_4+x_5+x_6\)

قیود
| قید | رابطه| |------|----------------------| | \(C_1\) | \(x_6+x_1 \geq 4\) | | \(C_2\) | \(x_1+x_2 \geq 8\) | | \(C_3\) | \(x_2+x_3 \geq 10\) | | \(C_4\) | \(x_3+x_4 \geq 7\) | | \(C_5\) | \(x_4+x_5 \geq 10\) | | \(C_6\) | \(x_5+x_6 \geq 10\) |