مدل‌سازی

مثال1

یک شرکت تولیدی قصد دارد رنگ های داخلی و خارجی ساختمان را تولید کند. این رنگ ها از دو مواد اولیه M1 و M2 تولید می‌شود.جدول زیر اطلاعات اولیه تولید رنگ را ارائه می‌دهد.

	رنگ خارجی	رنگ داخلی	ظرفیت روزانه انبار
ماده M1	6	4	24
ماده M2	1	2	6
سود	5	4

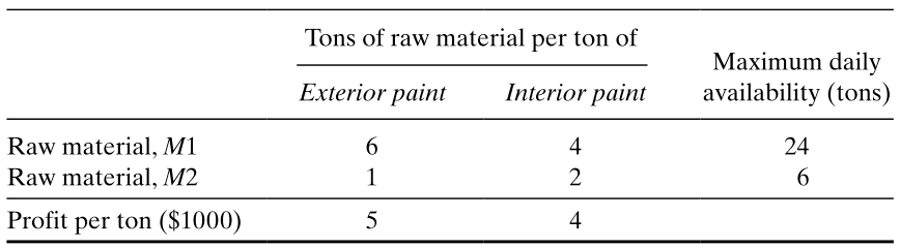
نیاز روزانه‌ی مصرف رنگ داخلی نمی‌تواند از مقدار رنگ خارجی بعلاوه‌ی 1 تن بیشتر باشد. همچنین بیشترین نیاز روزانه‌ی مصرف رنگ داخلی 2 تن است. این شرکت می‌خواهد بهترین نسبت تولید رنگ داخلی و خارجی با بیشترین سود را تعیین کنید.

1 جواب

متغیر مستقل

متغیر	شرح
\(x_1\)	داخلی
\(x_2\)	خارجی

متغیر وابسته

\(Z=5*x_1+4*x_2\)

قیود

قید	رابطه
\(C_1\)	\(6*x_1+4*x_2 \leq 24\)
\(C_2\)	\(x_1+2*x_2 \leq 6\)
\(C_3\)	\(x_2 \leq x_1+1\)
\(C_4\)	\(x_2 \leq 2\)

مثال2

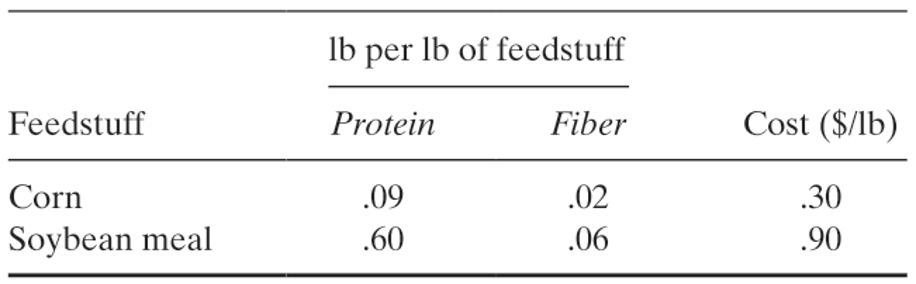
صنایع کشاورزی اوزارک نیاز به حداقل 800lb نوعی ماده‌ی غذایی دارد که از ترکیب ذرت و سویا بدست می‌آید. نسبت ترکیب به شرح زیر است:

	پروتئین در هر پوند به پوند	فیبر در هر پوند به پوند	هزینه هر پوند
ذرت	0.09	0.02	0.30
سویا	0.60	0.06	0.90

جواب 2

متغیر مستقل

متغیر	شرح
\(x_1\)	ذرت
\(x_2\)	سویا

متغیر وابسته

\(Z=0.3*x_1+0.9*x_2\)

قیود

قید	رابطه
\(C_1\)	\(0.09*x_1+0.6*x_2 \geq 0.3*(x_1+x_2)\)
\(C_2\)	\(0.02*x_1+0.06*x_2 \leq 0.05*(x_1+x_2)\)
\(C_3\)	\(x_1+x_2 \geq 800\)

با ساده‌کردن

قید	رابطه
\(C_1\)	\(-0.21*x_1+0.3*x_2 \geq 0\)
\(C_2\)	\(-0.03*x_1+0.01*x_2 \leq 0\)
\(C_3\)	\(x_1+x_2 \geq 800\)

قیود مخفی

\(x_1 \geq 0\)

\(x_2 \geq 0\)